
有限元方法与Thermal Desktop
下载PDF 文档
摘要
尽管计算机辅助设计技术取得了较大的进展,但有限元(FEM)软件还是不能用于航天器热分析,对有限元软件的主要抱怨是:
- FEM基于数学抽象,并非基于物理定律;
- FEM软件不能模拟热管、加热器等过程控制量;
- FEM软件在辐射分析能力上存在不足:
- 没有真实曲面(平面单元拼凑);
- 积分法不准确(不能计入多次折反射、遮挡、穿孔),
- 光线追迹单元太多(算不过来);
- 无热光学模拟能力;
- 对热分析而言,FEM模型又大又笨拙
- 热应力集中区可不一定就是高温度不均匀区。
- 在温度近乎不变的区域过多过密的单元会造成计算的不稳定。
- 不能模拟复杂流道、管网的流动和换热过程;
- 不能系统分析气冷、液冷、相变过程、低温制冷、压缩循环等热力学过程。
但是,并不能因为这些问题就否定有限元方法在热分析上的可用性,如果加以改进,基于FEM的热分析软件还是非常有优势的,尤其在兼容性和易用性等方面。
在本文中,从能量守恒的角度分析了FEM,说明有限差分(FD)和有限元是能在同一个模型内存在的,而且也能使用传统的求解器,如SINDA/FLUINT进行求解。
下面给出我们集成了有限元和有限差分的、能有效满足航天器热分析各领域需求的热分析软件的介绍。
简介
尽管有限元软件在与CAD和其它系统的集成方面具有优势,但在航天器设计方面很少用此类软件进行热分析,主要原因是这些软件不能模拟热控过程量,如热管、加热器等,另外在热辐射分析上存在缺陷或根本没有此项计算能力。(注:在流体应用逐渐增加的现代航天业,这些软件也不能模拟液冷、两相及压缩循环系统等)
由于航天应用需求相对较少,航天界自身又一直使用有限差分进行热设计,所以,FEM软件在航天器热分析方面不太适用是必然的。但是,只要加以合适的改进,FEM方法还是能在航天器热设计领域发挥作用的。
航天热设计对FEM软件的排斥来自两方面原因,一个是此类软件不能满足航天器热设计所有需求,另一个就是对FEM软件的误解。因此,本文的目的也有两个,一个是澄清一些概念,如FEM软件给出的负值热导问题。另一个是告诉大家,由于我们所做的工作,目前集成FEM方法的热设计软件已经完全满足航天热设计的需求。
基于能量守恒的FEM
FEM方法不能在航天业推广的原因之一是方法基于数学抽象,而不是基于物理基本规律。尤其是负值热导更是让人觉得这种方法有问题。
FEM方法的强处在于它在多工程领域的通用性和具有简化任何偏微分方程的能力,且简化带来的误差是可控的。
FEM方法的复杂性并不是让人更加信任它的理由,尤其是当使用简单的能量守恒方法也能实现分析目的时。可是,有限元的确在热分析中应用了能量守恒定律。
点源——考虑图1所示的有4个节点,1个点源(如激光束)的模型。由对称性知道,4个节点应当处于同一温度。合理的模拟方法是将热量平分,使得4个节点温度值相同。
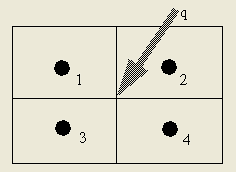
图1:节点交接处的热源
如果点源的位置稍有偏差的话,一般软件都会把热量单独规划到点源所在节点,这样在实际中几乎没什么变化的温度分布,就会在计算中就出现很大的偏差(如果做热光学分析,这将显着地影响应变分析结果)。
如果有上述现象出现,那么需要提高节点分辨率,但是,无论怎样细分,单独获得热源的节点温度还是会高于其它节点。
其实,并非必须通过增加节点数目才能提高精度,这种台阶形式的处理方法远不如平滑方法精确。如果热源位于多个节点的交点,平分能量就可以了;如果热源位于某个节点的中心,它就独享此热源的能量;如果热源分布情况介于这两个极端之间,那就需要根据彼此距离进行分配(图2),总之需要保持能量的守恒。
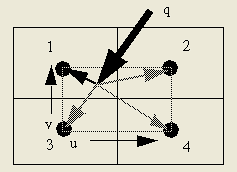
图2 能量在相邻节点间的分配
热源的位置可由两个介于0和1间的变量(u和v)描述,各节点分配的热流值等于总值q乘以公式(1)给出的相应系数。
 公式(1)
公式(1)
在任意位置处,系数总和为1,以确保能量守恒。根据与控制体中心的距离判断能量分配是FEM热计算的根本方法。事实上,所有的热源都是以这种形式确定的。
分布热源 - 假定图2节点承受的是分布热源,而不是点源,那么,分布热源也能通过细分并将每一部分简化为点源后,以上面同样的方式处理。例如,热源的分布规律为u和v的函数,则节点2得到的热量为:
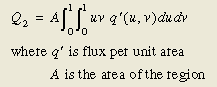
这个公式是单位面积热流与节点2的分配函数(公式1)的乘积在整个区域内的积分。
传统的控制体能量分布方法可以视作能量分布函数的一个特例——阶跃函数,在控制体内分布函数为1,其它地方为0,对于在整个积分域内分布函数为常值的工况,采用公式(1)的分布函数求得的结果与传统的阶跃函数分布方法一致。
热容 - 节点的热容同样也能利用上述的能量分配方法得到,偏微分形式的导热基本方程本身阐述的也是内能变化速率与导热和体积热源造成的能量积累间的关系:
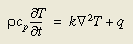 公式 (3)
公式 (3)
可以看出公式的每一项都具有同样的单位——体积热流率。偏微分形式的导热方程将公式的所有项都处理为点源。我们可以利用平滑变化的能量分布函数确定由于储热造成的节点能量平衡公式的变化。
例如,采用图2所示的内插区域,由于显热造成的节点2能量平衡公式的变化如下
 公式 (4)
公式 (4)
中括号内的项是节点2在整个内查面积内的热容。如果密度和比热保持不变,积分的结果是节点2具有整个热容量的1/4,与采用阶跃函数得到的结果相同。节点2的总热容量还应包括其它含有节点2的所有内查区域。
导热 - 在某一点处由于导热积累的净能量可被分配到每一个节点。再次使用图2的例子,以导热方式进入节点2的净能量为:
 公式 (5)
公式 (5)
为简化讨论,我们可以采用符号Ni代表节点i的分配函数。我们同样也可采用Green定理[2]将公式5内的拉普拉斯项简化为梯度,从而得到以导热形式进入节点的如下能量方程:
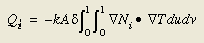 公式 (6)
公式 (6)
公式中分配函数的梯度 Ni指向节点中心。分配函数可被视作一个“帐篷”,在节点中心为1,在内查区域的边界处为0。梯度给出了增长最剧烈的方向。在取反向并点乘温度梯度后,给出的是以导热形式进入节点的单位体积热流率(需乘以导热系数k)。
Ni指向节点中心。分配函数可被视作一个“帐篷”,在节点中心为1,在内查区域的边界处为0。梯度给出了增长最剧烈的方向。在取反向并点乘温度梯度后,给出的是以导热形式进入节点的单位体积热流率(需乘以导热系数k)。
热源项和热容项对节点能量平衡方程的贡献可以直接求解得到,但是,由于导热项内包含温度梯度,所以我们必须采取假设使得温度梯度能以未知温度的函数形式表示,才能进行随后的积分运算。
在内查间隔上给出温度梯度的近似表达,可以首先从温度值的近似表达开始,
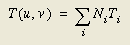 公式(7)
公式(7)
可以看出,用公式(1)给出的分配函数替代公式(7)中的项,上面的公式将是节点中心温度在整个内查区间的简单2维插值。因此,给出温度梯度如下:
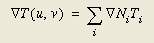 公式 (8)
公式 (8)
注意,在计算分配到某一节点的能量时,采用了与温度内查同样的函数。按有限元(FEM)的说法,使用同样的分配函数(权重函数)作为内查函数(形状函数)的方法称为伽勒金(Galerkin)方法。
伽勒金方法的特殊性在于节点能量平衡方程组内存在角对称项。用公式(8)替代公式(6)中的对应项:
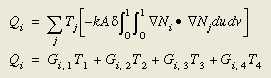 公式 (9)
公式 (9)
通过导热进入一个节点的净热流值由4个未知温度构成的代数方程决定。此外,由于存在对称性,Gij=Gji。还由于在内查区内的每一点上内查函数和为1,因此有如下方程成立:
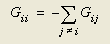 公式(10)
公式(10)
因此,节点i的能量平衡方程中的导热项也可以下面熟悉的方式表达:
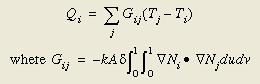 公式 (11)
公式 (11)
负值热导 - 对于已经适应了集总参数电路类比方法的热工程师而言,FEM热分析带来的最难理解的概念之一就是,在某些类型的内查区间上,主要是钝角三角形,会出现负值热导。这常常成为人们拒绝采用FEM进行热分析的理由,因为负值热导被认为是违反物理常规。但是,必须认清的是,在2个节点间由有限元方法(FEM)产生的导热项并不代表2个节点间的热量传输。公式(11)中求和的导热项代表了热节点的总能量平衡。而进入节点的净热量是以温度的线性组合形式给出,并调整为SINDA/FLUINT[1]兼容的格式,这种格式看起来有些像热导(conductors),但实际上它们不是。
让我们考虑一个简单的例子,以正确认识某一节点的全局能量平衡和节点间存在的单独热流率间的区别。传统的质心方法(centroid approach)以代数式逼近导热方程中的积分项:
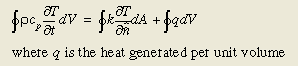 公式 (12)
公式 (12)
公式(12)中的积分项被转化为代数式的求和项,微分项近似为差分项:
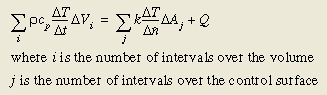 公式 (13)
公式 (13)
左侧的求和过程通常只是在整个控制体的一个积分步长内进行。中值定理告诉我们评估积分的最好位置是在体积元的质心。质心方法也称作"finite-sum-finite-difference"方法。
对于矩形节点,公式(13)右侧的求和可分为4段,对应于每一个表面。垂直于控制体表面的温度梯度近似取为相邻节点间的温差与间距的比值(图3)。请注意联结2个节点的连线必须垂直于控制体表面以满足准确近似需求。采用余弦投影方式并不能保证一直产生精确的结果。
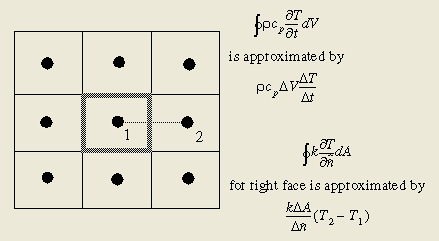
图3: 导热方程的Centroid method近似方法
在公式(13)右端的求和项中,将每一个面分成多段能够进一步发展此方法并给出通过控制面热流的更精确的近似表达式。下面的例子中,右端面被分成2段(图4)并且给出了每一段内垂直于控制面的温度梯度近似公式。在导热项的模拟中,这个方法可被视为二次质心方法。
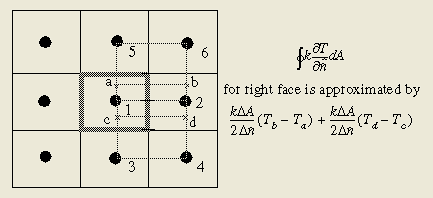
图4: 分成2段的Centroid method方法及右端面的导热热流近似。
我们能再次采用内查域方法评估a、b、c、d点的温度,以便计算垂直于控制面的温度梯度值。考虑具有单位厚度、单位长宽的正方形控制体,右端面热流的代数近似式如下:
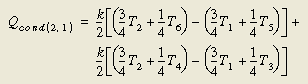 公式(14)
公式(14)
从节点2到节点1的热流可表达为6个节点温度的函数,而不再是节点1和2。这种表达式能被代数变换为热导"conductors"形式:
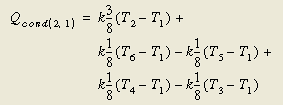 公式(15)
公式(15)
此时,我们在节点1到5间、节点1到3间有了负值热导,这并不意味着在这些节点间存在负能量流动!在节点1和2间的热流率由一系列热导所决定,而不是单独一个。代数公式的调整只是为了满足与热求解器(如SINDA/FLUINT)输入兼容的要求。一旦这些数据被SINDA/FLUINT读入,进行的数值计算与公式(14)是等价的。
需提醒的是,在公式(14)中只有T2和T1能以类似典型热导的形式重新安排。T3和T6是通过人工添加补充项才使得其表观上类似热导。这些人工添加的补充项的总和为0,以保持与原方程的一致。
为完备节点1的能量平衡公式,通过其它表面的热流必须也被计入。当所有的热导迭加在一起的时候,形成了图5所示的网络。

图 5: 采用基于控制体的有限元方法得到的热导
在这个简单的例子中,两个节点间的热流率以负值热导的形式出现。每一个表面的热导能直接输入到SINDA/FLUINT中,也可在多项求和后输入。
此方法能应用在任意四边形区域上,用公式(8)计算控制域边界中心点的温度梯度的方法被称为基于控制体的有限元方法(CV-FEM)[3]。在这个正方形控制体内,总热导值为正,因为负值热导被大的正值热导抵消了,但对于倾斜三角形几何而言,情况有可能出现变化。
即使代数表达式给出净值为正的热导,它们也不能被视作代表两个节点间以导热方式传递的热量。图5中中心节点与对角节点间存在正值热导,但是,没有热量会直接从中心节点传递到对角节点。因此,如果需要得到任意2个节点间热流的确切值,必须采用未作变换的公式(14),并使用计算得到温度值才能得出。
对于形状规则的内查域,产生的热导将是正值。当区域高度扭曲后,会产生负值热导。联想到导热热流是以单元上内查得到的温度表示的,当单元扭曲后,会出现外查。例如,如图6所示的简单1D有限差分外查温度问题,表面温度存在负号项。外查,而不是内查,同样也会出现在有大的内角的2维区域,造成负值热流含义项的出现。
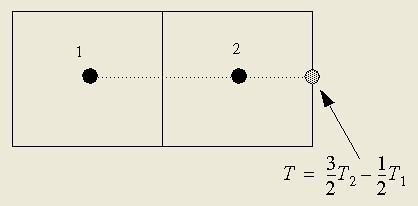
图 6: 外查产生负值项
大的或高度扭曲的单元会产生负值热导,但这并不一定就意味着出现了严重的错误。更主要的判据还是要看实际温度在整个内查区内与所做温度变化的假设的匹配程度。四边形区域意味着温度变化是双线性的。三角形区域意味着温度变化是单线性的。
Costello[4]已经开展了一系列“热补丁”实验,将任意形状的三角形单元镶嵌到大的矩形区域内。将补丁一面设置为0,另一面设置为1,并用有限元产生的热导网络计算穿过补丁的净热流。在对比计算值与理论值后发现,在所有的内角值下,甚至是产生负值热导的钝角三角形内,结果精确匹配。
在这个例子中,解沿着“补丁”呈线性变化(一边为0,另一边为1)。用于三角形的线性近似方法已经足以精确匹配这个例子,即使对于高度扭曲、产生负值热导的单元也同样如此。
Costello也指出了一个与有限元方法相关的明显的佯谬。他考虑的是如图7所示的三角单元。由于这是一个钝角三角形,节点1和3之间会存在负值热导。假定节点1固定在0度,节点2固定在1度。想通过加热使得节点3温度维持在1度。由于节点3的温度与节点2相同,在3和2之间应当没有热量传递。由于节点1和3间的热导为负值,必须从节点3上移走热量,而不是添加到节点3上才能使得其温度维持在1度。
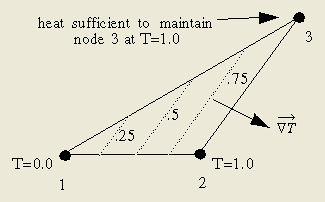
图7: 三角形FEM单元的不恰当使用
解释这个问题需首先考虑在这个单元上所做的假设。三角形单元意味着节点间温度呈线性变化。在这个例子中,3个节点的温度已经被指定,因此也指定了单元内部的温度梯度。在这些特定温度作用下,梯度将垂直于节点2和3构成的表面,对于一个三角单元,在内查区域内温度梯度都保持恒定的情况下,等温线的分布如图7所示。
如果三角单元是镶嵌在一个大的网络单元内部,给出的梯度分布可能是合理的。但是,在这个特定的热问题中,三角单元的边是隔热的,并且实际的等温线必须垂直于边界。真正的温度解与三角单元使用的假设区别很大。使用多个单元(如将三角单元分成两个小三角形会明显改善结果),或根据预估的求解形式手动产生导热项将是比较好的解决办法。
图7例子中还有一个值得注意的地方。由于节点1和节点3间存在负值导热项,所以应当会存在负的能量流动,这是违反物理常规的。我们还需要考虑所有的热导以便计算出某一单元上所有节点间的热量流动。考虑下例的控制体:
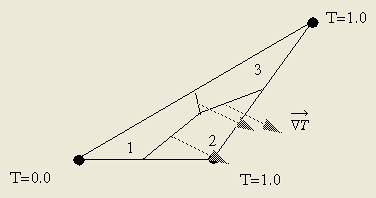
图 8: 三角形单元控制体的热量流动
在先前假定的温度下,梯度垂直于右端表面并在单元内保持恒定。温度梯度绘在个节点控制面的中心。定性地,可以看出热的确是从节点3流动到节点1,同样的,热量也从节点2流到节点3,尽管两者处于同一温度。如果这个单元处在大的网络中并且这个梯度实际存在,那么实际上会有热量从这个表面流出。
在预计例子的可能答案时,我们也会猜想到温度梯度会从节点1指向节点3,几乎垂直于我们选定的单元和温度条件下的梯度。热量必须从节点3处移走,不仅因为负的能量正从节点1流出,而且还因为从节点2流出正的能量。
电路网络类比虽然在帮助理解传热过程方面非常有用,但它并不对所有热问题都有效。一些热问题能以等效电路网络形式提出,但是,并不是所有的热问题都满足集总参数电路网络类比的条件,不是因为负值热导违反物理常规,而是因为这种问题几乎不可能建立集总参数电路类比网络。
考虑到有限元方法,热导可以看成能量守恒方程代数变换的副产品。它们是导热项调整后形成的“热导”项。在模拟时牢记能量守恒方程,并掌握微分和积分项用代数式表达的办法能避免走弯路,也有助于全面地认识和使用各种模拟方法。
与有限差分(FD)方法的兼容
矩形区域内的能量平衡方程各项(热源、热容和导热项)的简化形式已经给出。对于任意形状的区域,必须在积分内包括Jacobian项以便建立dudv单元与实际面积间的联系。内查函数Ni的梯度,也必须从u,v坐标系转换到x,y,z空间。但是,这里强调的不是用有限元(FEM)或控制体(CV-FEM)方法产生能量平衡方程各项系数的机理,这些工作用计算机做要比手算快得多,而且详细的信息在参考文献[5]内也有介绍。
这儿的目的是提供一种基于能量平衡理论的方法,以便清晰给出FEM与FD、与传统的求解技巧、辐射分析间的结合方式。FEM可被视作一种将能量源根据与控制体中心的相对距离分配到节点上去的技巧。分配函数是任意的,但是选用线性内查分配函数给出的结果是最简单的。在导热方程中的外部热源、热容、导热项都可以同样的方式处理。
FEM中的“单元”只不过是专门划出来供某一特定分配函数使用的区域。节点仍可视为代表控制体内某一位置、且具有其平均温度的特殊点。环绕一个节点的多个单元的中心可以连接起来构成热节点的控制体。
另外,在节点能量平衡公式中可以选择是采用阶跃变化的分配函数(FD)还是平滑变化的分配函数(FEM),来描述各种类型的组成项(热源,热容、导热)。例如,考虑图9中所示几何。

图 9: 进入某一节点的能量可用光滑或阶跃分配函数分配
一小片加热片放在节点6位置处。节点6的控制体可视为由节点周边所有单元中心连线构成。控制体的热容量可根据此体积计算,或用公式(4)计算。加热片释放的能量可被视为全部进入节点6,或用平滑变化的分配函数将能量分布到单元的各个节点。
使用有限元方法,加热片能被细分为小区间,然后每一区间的热量根据分配函数分布。但是这并非必须采取的步骤。如果这部分模型是手动建立的,那么细分加热片并将热量分配给相关节点带来的精度的提高可能并不值得费力去做。这种情况下,将热量集中赋给节点6是最好的工程简化手段。
单元定义好后,计算机会自动产生导热和热容项,避免了手工计算的劳累和容易出错的缺点。如果部分模型不是以几何体表示的,那么用有限差分产生的抽象节点也能与FEM网络的任何节点连接构成新的热导。
例如,假定图9中的网格代表了一块平板,节点12与节点11间的连接代表了板安装位置处的热量泄漏。热量泄漏主要由支承、绝热垫和螺栓造成。对这个模型而言,使用抽象简化比建立支承件的详细FEM模型更合理些(虽然可以建立详细的有限元模型以检验抽象简化的可用性)。
FEM模拟方法的应用并不排斥其它模拟方法,时刻考虑到FEM方法的能量平衡可使得热模型兼容FEM和FD。在保持与CAD几何一致性的同时,FEM也大大提高了模拟的效率。在几何体不存在或用FEM表示不太恰当的地方,FD方法可被应用。FEM方法应当被视为一个能完善,而不是排斥现存FD方法的模拟工具。
与SINDA/FLUINT的集成
如公式(2)、(4)、(11)所示,采用FEM产生的节点能量平衡项与SINDA/FLUINT直接兼容。任何采用线性内查的1D、2D或3D单元将生成兼容的热导和热容。
过去常认为SINDA/FLUINT是个有限差分、电路类比型热分析器。这种观点可以接受,但更准确的描述是,它是一款通用的等式求解器。并可无需改动地直接接受FEM产生的系数,这样,将求解器绑在FEM程序上造成的大多数抱怨都可通过舍弃那些落后的软件简单地得到解决。
如同前面讨论的,如果节点间的热流需要计算的话,必须在SINDA/FLUINT中加入必要信息。有限元前处理器能自动产生数据文件和计算所需的子程序。而不需要在用户逻辑中获取温度和热导,手动计算节点间的热流。专门的程序能作为标准SINDA/FLUINT库函数的一部分提供给用户以自动完成此项功能。
另外一个对有限元方法的抱怨是,有限元网络难于根据实验数据进行调整。通过手动调整单个网络单元的做法很困难,因为一两个热导根本不能代表整个热流分布。在实验数据修正过程中,最好首先通过热流计算程序获取足够的模型信息后,再调整厚度、热导率、比热或原来的有限元几何形状来实现。
为实现有限元单元与热分析器,如SINDA/FLUINT间的集成,我们也在其它方面做了很多的工作,工作的目的是用单元质心法将有限元单元转换为有限差分的形式。
完成有限差分转换的部分动机是想让程序产生我们所熟悉的网络形式,因为许多分析者对有限元有负面印象。但完成这种转换的更主要目的是想实现热模型与现有热辐射分析工具间的兼容。在有限元的基础上形成热网络使得在有限元软件和传统热辐射分析软件,如TRASYS[6]或TSS[7]间更容易建立一致的界面连接。
转换有限元网络到某种形式的有限差分格式的确能实现有限元与现有热辐射分析软件间的兼容。但是也有其它缺点,如同公式(13)所示,质心方法的精度依赖于连接质心的连线与单元边的垂直关系。单元的扭曲会造成很大的误差。采用余弦缩放比例方法也并不能保证结果的正确性(如图10所示)。
任意方向的温度梯度取决于温度梯度矢量在此方向的投影。在所示的例子中,用两个节点近似得到的梯度余弦明显小于垂直于控制体边界的实际的梯度。控制面投影的方法也会产生同样的错误。如果实际的温度梯度与连接节点1和2的连线方向一致,则不会出现任何错误,但是随着温度梯度与中心点连线间夹角的增大,误差也会增大。
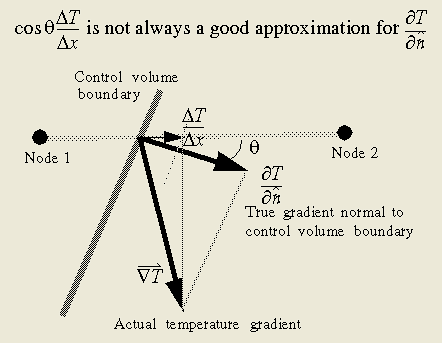
图10: 当节点间的连线不垂直时产生的热流误差。
后处理和不同模型间数据的匹配也是采用质心方法后必须面对的一个难题,单元值必须被转换回节点值,节点值一般都是取连接此节点的所有单元的平均值。这必然会造成了人为的数据平滑效果。
另外一个方法就是在每一个单元的中心放置一个附加的节点,然后用更小的FEM单元连接此节点和已有的节点。中心节点用于辐射热传递。这是一个很有用的办法,但是产生了很多附加节点。
FEM单元与传统热分析软件最有效、最直接的集成方法就是原封不动地使用它们。兼容性问题不是出在有限元上,而是出在热辐射分析软件上。最好的办法是对热辐射分析软件进行修正,而不是把精力放在处理FEM向FD单元转换过程中出现的问题和不足上。
与辐射分析集成
航天热分析者不仅关心导热,更主要的还是关心航天器表面间的辐射热交换以及轨道外热流的加热效果。但这些计算通常会比单纯地计算温度分布要消耗多得多的计算机资源。FEM方法在航天热控应用中非常受限的原因之一可能就是因为没有合适的辐射分析工具与之结合。
就像前面讨论的,在FEM网格上的节点可以仍按照传统的控制体方式理解,或采用一个光滑变化的能量分配函数来描述。辐射交换能通过TRASYS或TSS等程序,将FEM网格上的节点仍视作传统的控制体来计算。而每一个节点的控制面可以通过将单元细分为更小的多边形完成(如图11所示)。
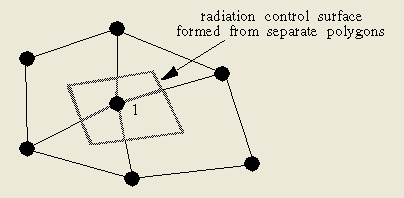
图11: 在FEM网格中将节点视作控制体进而产生热辐射交换表面的方法。
图11中的节点1将会产生4个独立的多边形供TRASYS和TSS使用(4个四边形构成包围节点1的大四边形)。这种办法会得到精确的结果,但是效率会降低,并且由于生成大量的表面将使得数据库文件增大。下一个办法可能会有更好的精度并且也符合FEM能量分配规律。
使用公式(2),可直接计算FEM网格上各节点的直接投入能量。这个方法在面积积分和蒙特卡罗方法中都适用。在面积积分方法中,单元被细分为小的区域,每一小的区域都视为一个点源。但这个方法尤其适用蒙特卡罗方法,因为每一根光线都被视为来自一点的能量束。由点源引起的能量沉积将根据与单元相联系的能量分配函数分布到各节点。
FEM网格间的辐射交换系数也能直接计算,使用与内查单元内部温度分布[7]同样的能量分配办法[8]内查单元内部的辐射率(图12),可在FEM表面上实现非等温辐射,而不再是简单的等温发射,这在同样尺寸的节点区域上会产生更准确的结果。
在这个方法中,离开一个单元的任一根光线所代表的能量束包括了单元上所有节点的贡献。内查函数的用途是确定在这根光线中每一节点的相对贡献。此项技术能直接得到所有的节点到节点间的辐射交换系数,也避免了从单元到节点的转换难题。这种方法同样也被集成到ESATAN/ESARAD[9]。
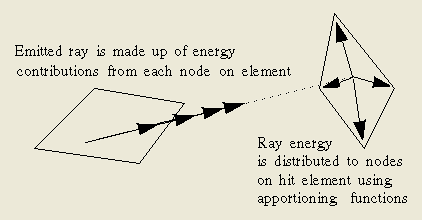
图12: 使用有限元方法的光线追迹
换而言之,如果不考虑光线能量由每一个节点组成,也可以在某一时间段单独计算一个节点的辐射能量,此时内查函数只是用于确定单元上光线的发射位置。使用这种办法,每一个根光线将只具有一个节点的能量值,但是在靠近节点位置处还需发射更多的光线,以避免出现大的误差。
以均匀化方式模拟表面辐射,和传统的等温面假设一样,等价于用阶跃变化的阴影色板显示几何模型,每一小单元都呈献单一色调的颜色。而使用非等温FEM网格方法,表面辐射则等价于使用光滑变化的“语音矫正法”,该凹的凹、该凸的凸,而不再是拼图般的感觉。
事实上,航天热辐射方法已经被用到计算机图形学上,用以产生极端逼真的图像[10]。图形学中图像产生问题与热辐射问题极端相似,除了一点——图形学关注的是离开表面的辐射能量(进入人眼的),而热辐射考虑的被表面吸收的能量。目前已经有很多的方法提出,其中包括在有限元中应用传统的双面积分的方法[11]。这是一个活跃的研究领域,有可能产生适合于热辐射分析的更好的算法。
需再次强调的是,辐射分析软件并非必须基于FEM。将传统的平面或二次曲面的“单一辐射率”表面和任意形状的“非单一辐射率”FEM网格兼容起来的软件能被设计出来。使用FEM构建辐射模型也并不排斥传统技术。一个集成了这些特点的、新的辐射分析软件RadCAD [12]的开发正在进行中(注:现已商品化投入市场)。
[12]的开发正在进行中(注:现已商品化投入市场)。
一个更好的有限元产生器
能直接利用FEM网格且可生成节点热流率和辐射交换系数的热辐射分析软件一旦开发成功,我们就能在SINDA/FLUINT中直接使用FEM产生的导热和热容网络(这是FEM软件的强项)。
但是,还有一个不足仍然存在,采用传统的辐射分析软件,圆柱面能够以很少的柱面节点来模拟,但是使用现有的FEM网格生成工具,必须用大量的平面单元才能实现柱面的几何近似。节点数目的多少完全取决于几何相似度,而不是热计算应考虑的计算精度。最后的结果是,你面对的模型是一个比传统的TRASYS和TSS模型节点数目多得多的热模型。
这是现有FEM软件的问题,而不是有限元方法的问题。现有的FEM软件所建立并发展起来的单元库类型主要是为了满足结构分析需要的(而不是为你的热分析而专门设计的)。
专门为航天热设计应用而设计的单元能够提出。在图2所示的例子中,一个简单双线性方案被用来拟合平面矩形单元上的温度变化。同样的内查方案也可用在图13中包覆在圆柱面上的矩形区域上。
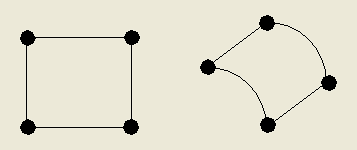
图13: 产生与柱面单元同样的热容和热导项的平面单元
你可以设想一个矩形平板,在一定的边界条件下得到某一特定的温度分布。只要曲面不被延展,这个分布就不会随着平板被折迭或被弯曲而变化。从拓扑学上讲,在计算热容和导热项时,曲面与平面是完全一致的。
有限元方法可以应用在曲面的任意区域(即使是“延展”区域),只要在这个区域上能够提出合适的温度分布内查方法。那些正在使用的、为人熟知的基本单元,如锥面、球面、环状面等,可与有限元方法同时使用。如果此类单元类型可用的话,就能在不增加单元数目的前提下建立热FEM模型。
另外,单元并非必须平行于表面的主参数方向。目前的软件允许柱面等表面按照恒定的高度和角度线细分。提高模拟的灵活性可以首先通过指定柱面的大致朝向和尺寸,然后用3个或4个参数(高度、角度)界定区域,用基于参数坐标,而非x,y,z坐标的三边和四边曲面单元拟合曲面。辐射分析软件首先判断光线与哪个几何体相交,然后再决定与这个几何体的哪个单元相交,然后才将相应数量的能量分配到此单元的节点上。
对热计算而言,曲面单元很简单就能实现,但是对应力分析和动力学计算而言,曲面单元的出现却会使事情变得非常复杂。折迭状态的纸在应力作用下的行为与平放的纸截然不同,这是为什么只有平面单元在现有FEM软件得到广泛应用的主要原因。
专门满足航天热设计需要的基于FEM的网格生成程序可以包括其它类型的特殊单元以帮助航天器热模拟。就像在应力分析中用到的一些特殊(抽象)单元,如阻尼器、弹簧、集中质量等,我们也能创建特殊的热单元,如加热器、热管、接触热导和多层隔热材料(MLI)包覆等。特殊的单元能被用来模拟给定区域上的特定的差分公式,也能用来代表模型中更为抽象的、或用过程量(用户逻辑)表示的部分。构成热模型的“组件”,有的用于生成数据和SINDA/FLUINT逻辑,有的用于使用有限差分(FD)方法生成热质量和热导,有的用于使用有限元(FEM)方法生成热容和导热项。
在一个名叫Thermal Desktop [13]的软件中,这些新的有限元(FEM)技术正与传统的模拟方法实现集成。Thermal Desktop将是世界上第一款将传统的有限差分方法、为满足航天热分析需求而专门做了改进的有限元方法、非几何方法集成到单一的CAD系统中去的软件。
[13]的软件中,这些新的有限元(FEM)技术正与传统的模拟方法实现集成。Thermal Desktop将是世界上第一款将传统的有限差分方法、为满足航天热分析需求而专门做了改进的有限元方法、非几何方法集成到单一的CAD系统中去的软件。
总结
FEM软件在航天领域的应用受到限制的原因包括,模型文件的庞大降低了计算的效率;不能提供必要的过程控制量的模拟;不能提供足够的辐射分析能力。目前由于需求较少以及航天界对有限元方法的负面印象,使得有限元软件供应商没有动力拓展现有软件在这些方面的能力。
由于与辐射分析软件不兼容,使得早些时候将FEM网格与已有热分析工具结合起来的设想一直未能实现。而解决这一问题的比较好的办法是修正当前辐射分析软件的不兼容性,而不是实现FEM网格的某种精确和有效地转换。
在有限元方法中考虑能量守恒定律,并结合当前的过程控制和有限差分模拟实践,将会使得FEM这个已使用多时的模拟技术真正成为热分析者喜爱的工具。在详细地考察了负值热导产生的物理过程、以及与此相关的代数近似式后,会发现用FEM和高次有限差分产生的热导并不单纯代表2个彼此连接节点间的热流流动,而是代表了多个节点间的热流流动的综合效应。
在现有的FEM网格生成器上加入二次曲面单元的模拟能力将使我们在保持现有节点密度(模型大小)的基础上,形成导热/辐射一体模拟的能力。允许任意朝向的曲面单元并增补一些特殊的模拟单元,如多层隔热材料(MLI)包覆、加热器等,也赋予了建模者崭新、强大的建模能力。
表1总结了这篇文章的主题,找出了经常在航天界被引用的有关FEM程序的问题(负值热导、辐射、模型大小、过程量的描述等),并给出了解决办法。一旦航天热工程师能真正了解有限元,并且被装备了能满足热控独特需求的、发挥了FEM软件独特优点的、新的分析工具,那么他们会发现他们已经获得了CAD集成技术和多系统并行工作的能力,如果非要找出失去了什么的话——只是手工建模的辛苦。
表1:总结
| 问题 |
解决方案 |
| 负值热导(未基于能量守恒定律,而且违反了热力学第二定律) |
错误概念 |
| 缺乏过程量的模拟 |
SINDA/FLUINT类程序可直接利用FEM产生的网络。 |
| 不适合辐射分析 |
开发出能利用有限元的热辐射分析工具 (RadCAD ) ) |
| 对热分析而言,模型太大 |
开发出能利用热单元的有限元软件(Thermal Desktop ) ) |
| 不适合热分析需求的求解器 |
继续使用SINDA/FLUINT类快速计算程序 |
致谢
Thermal Desktop软件的研发得到了NASA Marshall Space Flight Center的资助,Bill Till先生为该项目的技术监理。
参考文献
- Cullimore, B.A., "Advances in SINDA/FLUINT and SINAPS," 26th ICES Conference, 1996
- Kreyszig, E., Advanced Engineering Mathematics, Fourth Edition, John Wiley & Sons, New York, 1979
- Schneider, G. E., and Raw, M. J., "A New Control-Volume-Based Finite Element Procedure for the Numerical Solution of the Fluid Flow and Scalar Transport Equations," Final Report to Atomic Energy of Canada Limited, Chalk River, Ontario, January 1986
- Costello, F. A., and Costello C. F., "Node Geometries and Conductances in Spacecraft Thermal Models," SAE paper 951698, 25th ICES Conference, 1995
- Zienkiewicz, O. C., and Morgan, K., Finite Elements and Approximation, John Wiley and Sons, New York, 1984
- Lockheed Engineering and Management Services Company, "Thermal Radiation Analysis System Users Manual," JSC 22964, Contract NAS 917900, October 1991
- Panczak, T., et al., "Thermal Synthesizer System: An Integrated Approach to Spacecraft Thermal Analysis," SAE paper 911582, 22nd ICES Conference, July 1992.
- Chin, J. H., Panczak, T. D., and Fried, L., "Finite Element and Raytracing in Coupled Thermal Problems," Proceedings of the Sixth International Conference on Numerical Methods in Thermal Problems, pp. 683-701, Pineridge Press, Swansea, U.K., 1989
- Cook, G. M., Hodgetts, C., Stock, N. J., Planas Almazan, P., "Using Finite Element Discretisation for Spacecraft Thermal Analysis," SAE paper 951608, 25th ICES Conference, 1995
- Sillion, F. X., and Puech, C., Radiosity and Global Illumination, Morgan Kaufmann Publishers, Inc., San Francisco, California, 1994
- Zatz, H. R., Galerkin Radiosity: "A Higher Order Solution Method for Global Illumination," Computer Graphics Proceedings, ACM SIGGRAPH, 1993
- Panczak, T., and Ring, S., "RadCAD: Integrating Radiation Analysis with Modern CAD systems," Presented at the 26th ICES conference, July 1996.
- Panczak, T., and Ring, S., "True Computer Aided Thermal Engineering: A Geometric and Nongeometric Simulation Environment," Final Report for NASA/MSFC, Contract NAS8-40666, July 1996
有关此主题的详尽信息,请联系作者:
Tim Panczak
C&R Technologies, Inc.
9 Red Fox Lane
Littleton, Colorado 80127-5710

