|
|
| Cool Software |
|
Hot Engineering |
与TRASYS模型的比较
隔离问题
在对比TRASYS辐射换热系数计算结果和蒙特卡罗光线追迹辐射换热系数计算结果之前,关注一下两者内容有何不同也是必要的。Gebhart算法和蒙特卡罗光线追迹算法所依据理论的差异会导致不同的计算结果。光线追迹法只要样本(发射光线数)足够多,计算结果都将趋势正确值。但是,Gebhart方法在模型未正确节点化时,会给出偏差很大的结果。考虑以下例子:
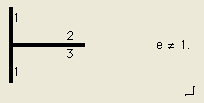
图1 – 隔离问题
Gebhart方法将计算面1到面2、面1到面3的角系数,在计算辐射换热网络时,将给出面2到面3的辐射换热系数(RADK),这是在真实情况中不可能出现的现象,造成这种问题的原因是“辐射过程波及全部节点”假设。在蒙特卡罗方法中,离开面2的一根光线击中面1后,在交点位置再次发射,那么,这根光线只能反射回面2或进入空间,因此,光线追迹方法不会有面2到面3的辐射换热系数。
节点化问题
下面的例子能很好地说明节点化在Gebhart计算结果中所起的重要作用。
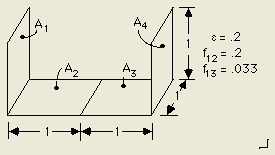
图2-节点划分造成的偏差解释例子
在上面的模型中,TRASYS给出的辐射换热系数RADK为3.36e-3,如果用户在SURFACE data block将面2和面3合并,辐射换热系数变为3.77e-03,节点划分差异造成的偏差为 12%。TRASYS角系数计算结果与理论结果一致。蒙特卡罗光线追迹给出的值是3.28e-03,这个结果不依赖于面2于面3的划分形式。对比光线追迹与Gebhart方法的计算结果是非常有意义的,如果两个结果相差较多,您也不会过于惊讶了。
角系数计算 考虑图3所示几何:

图 3 - TRASYS 角系数计算
下表给出了TRASYS计算结果与理论计算结果的对比,非常有趣的是数据中好像有个介于6.6和6.7间的魔力数字,使得TRASYS给出更准确的计算结果。看到这儿人们不禁疑惑,是否还有其它什么没公开的魔力数字使得模型出现问题呢?
L/d |
Closed Form |
TRASYS |
%Error |
10. |
.2819 |
.3805 |
35.0 |
6.7 |
.2765 |
.3498 |
26.5 |
6.6 |
.2763 |
.2731 |
1.2 |
1.0 |
.2000 |
.2000 |
0.1 |
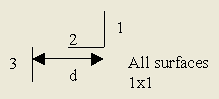
图 4 - TRASYS很差的遮挡计算能力
通过改变距离d,对比了TRASYS和蒙特卡罗法计算的从面1到面3的角系数值,见下表数据,其中蒙特卡罗法的计算光线为十万根,结果可认为相当精确了。
d |
蒙特卡罗法
VF1-3 |
TRASYS
VF1-3 |
百分比误差 |
1.5 |
.01871 |
.01689 |
-9.8 |
1.9 |
.02315 |
.01284 |
-44.5 |
2.1 |
.02399 |
.03447 |
+43.7 |
2.5 |
.02317 |
.02719 |
+17.3 |
TRASYS计算结果偏差的原因是软件判断遮挡的算法问题,在小d值下,TRASYS过高地估计了遮挡的效果,在大d值下,TRASYS不再计入遮挡,因此角系数值又太高了。
Gebhart算法 – 误差传递
Gebhart算法会传递来自于角系数计算的误差,考虑图5中的几何体。
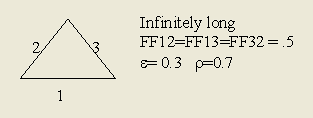
图 5 – Gebhart误差传递模型
Gebhart求解器运行了两次,一次角系数为0.5,一次角系数为0.49,误差为2,辐射换热系数及误差值如下,
| |
Gebhart, vf=.5 |
Gebhart VF=.49 |
%Error |
B11 |
.259 |
.239 |
7.7 |
B21 |
.370 |
.349 |
5.7 |
B31 |
.370 |
.349 |
5.7 |
RK Sum |
.999 |
.937 |
6.3 |
列出以上问题的目的是使TRASYS用户能意识到他们的模型一直存在一些错误,但是仍能得到较为准确的结果。 而蒙特卡罗用户也不必动则发射数以百万计光线以谋求0误差。
|

